참고 URL : http://blog.naver.com/leojesus?Redirect=Log&logNo=80021067736
Bellman Ford & Dijkstra Algorithm for Routing
Written by windwiser
[불펌은 금지 ~]
Network Review doc #1
지금부터 다시 Posting시작 ~
[틀린 부분 덧글로 달아주세요 ~]
동적 혹은, Adaptive즉, 적응적 Routing기법 알고리즘등으로 불리는 유명한 알고리즘에 대해 공부했던 내용을 Review한다.또한 Dijkstra’s Algorithm에 대해서도 언급하고 있다.
Picture 1. adaptive routing
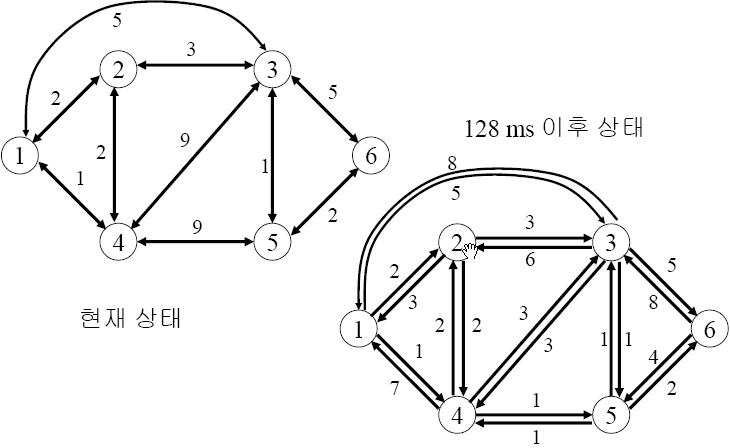
6개의 Node로된 Network를 가정해 보자. 각 인접 Node끼리 정보를 주고 받고 있다.
그 정보라는 것은 바로 최적경로상의 인접Node가 무엇인가라는 것과, 자신을 기준으로 했을때의 다른 Node로 가기까지의 최소 전송 지연시간에 대한 정보이다.
이 Network에서는 경로배정의 결정이 각 Node에서 일어나는 Distributed구조이다.
지금부터, 128ms 후에 서로 주고받은 위 2가지 정보
- 특정Node까지의 최소 지연시간
- 최적 경로상의 인접노드
를 이용하여, 새로운 각 Node별로의 Routing Table을 만들어 보자.
128ms후에 Node 6에서 받게 되는 망 정보라는 것은 바로 인접 노드인 3,5로부터 받는 정보이다. 이 정보는, 3,5node를 기준으로 하여, 나머지 모든 node로 가는데 걸리는 최소지연시간 정보이다.
현재의 Node 6의 Routing Table을 만들어 보자. 그리고, 128ms후에 인접 Node 3,5에서 보내주는 최소 지연시간 정보까지 정리해 보자.
|
목적지 |
지연 |
다음Node |
From node 3 |
Form node 5 |
|
1 |
8 |
5 |
7 |
6 |
|
2 |
6 |
5 |
4 |
3 |
|
3 |
3 |
5 |
- |
1 |
|
4 |
8 |
5 |
2 |
1 |
|
5 |
2 |
5 |
1 |
- |
|
6 |
- |
- |
3 |
2 |
Table 1. recent routing table of Node 6
Node 6의 현재(before 128ms) Routing정보를 보면, 위와 같다. 화살표를 따라 나온 숫자는 최소지연시간을 의미한다. 위 black box된 정보가 두 인접 Node인 3,5에서 온 정보에 의해 어떻게 변화되는지를 알아보자.
먼저 Bellman-Ford Alogorithm으로 생각해 본다면,

Picture 2. Bellman Ford Alogorithm
계속적으로 애기하고 있지만, Bellman Ford Algorithm은 Distance vectior routing Alogorithm중에 하나이다. 또 다른 말로는 Adaptive routing방법중에 하나라고도 한다.
말이야 어찌되었든간에,
이놈은, ARPANET의 최초의 라우팅 알고리즘이었으며, RIP라는 이름으로 인터넷에 등장하였다.
또한 이런 의문이 들것이다. 앞서 예에서는, 최소시간지연을 적용하였는데, 앞서의 Distance vector라는 말과는 먼가 안맞다고 말이다. 하지만,
실제, 이 알고리즘을 적용함에 있어서,
시간일수도, 거리일수도 있다.
즉, Node가 이웃한 Node 각각에 대한 “거리”를 알고 있다고 가정하고 시작하는 알고리즘이다. 아니면, “시간지연”을 알고 있다고 가정하는 것이다.
그럼 다시 돌아가서,
128ms후에, Node 6의 Routing Table이 어떻게 변화되는지 주목해 보자.
l63 = 5, l65 = 4 : l은 목표 node까지의 현재 최소지연 시간이다.
i) i=3, d61=l63 + d31 = 5 + 7 = 12
ii) i=5, d61=l65 + d51 = 4 + 6 = 10
so, d61 = 10 128ms후에 Node 6에서 1로의 최소 지연시간은 10로 설정되며, 인접노드 즉, Routing경로상에서의 인접 Node는 5가 된다.
Node 4로의 경우를 따져보면,
i) i=3, d64 = l63 + d34 = 5 + 2 = 7
ii) i=5, d64 = l65 + d54 = 4 + 1 = 5
so, d64 = 5 128ms후에 Node 6에서 4로의 최소 지연시간은 3으로 설정되며,인접노드 즉, Routing 경로상의 인접 Node는 5가 된다.
이처럼 모든 Node에 대해서 계산해 보면, 128ms 후의 Node 6의 Routing Table에 대해서 완성해 볼 수가 있다.
즉, Node 6에서 다른 어떤 목적 Node로 가기 위해서는 반드시 두 인접노드를 거치게 된다.
따라서, 반드시 인접노드와의 최소지연 시간에 대한 정보는 언제나 현재 시점을 기준으로 게산에 반영되어야 한다. 다음으로, 인접노드에서 보내온 최소지연 시간 벡터를 이용하여,
그 인접노드에서 목표 노드까지 걸린 지연시간을 더한다. 이때, 두 인접노드에 대한 크기비교를 통해, 작은 값이 해당 목표 노드에 대한 Node 6에서의 최소지연 시간으로 설정된다.
물론 이때의 인접Node가 또한 설정된다.
이것은 특정 한 Node에서의 인접Node를 고려한 후에, 그 인접Node에서의 주기적인 최소 지연시간정보를 얻어 옴으로써, 어느 경로를 타는 것이 최소의 시간이 되는 가를 Node에서 결정하는 것이다.
|
목적지 |
최소지연시간 |
인접Node |
|
1 |
10 |
5 |
|
2 |
7 |
5 |
|
3 |
5 |
5 |
|
4 |
5 |
5 |
|
5 |
4 |
5 |
|
6 |
0 |
- |
Table 2. Routing Table of Node 6 after 128ms

천재다 -_-;;
졸라 피곤해 보이시는 저 인상이 애처롭다;; programing나아가서 컴터 관련 모든 학문과 기술을 하나의 art로 보셨다는 그 분. 우리가 2002년 열라 world컵에 흥분할 그 시점에 지구 저편에서는 한 명의 천재가 숨을 거두었다.
Semaphore와 Dijkstra 최단거리 알고리즘으로 유명하시당 ..
Picture 3. Dijkstra
Dijkstra Algorithm
이 Algorithm은 최단거리를 알려주면서 동시에 최적경로(비용이 최소-여기선 비용의 요건으로 거리만을 생각)를 알려준다. 개인적으로, 이 알고리즘은 처음에 볼때는 그저 그랬다.
왜 그랬을까? 주위 사람들의 애기론 골때리는 알고리즘이라던데 말이다.쉬웠다 왜 일까?
그 이유를 자꾸만 생각해보다 보니, 내가 제대로 이해하지 못했다는 결론을 얻게됬다.
그래, 역시 엑기스를 뽑아 먹기가 그리 쉽나 -_-;;
개인적으로 Algorithm학문을 깊이 파본 경험은 없지만, 알고리즘을 생각하거나 만들 때,
어느 한 시점에서의 최적을 생각하여 그 부분적 최적의 합이 곧 전체 최적의 결과를 만들어 낼수 있다고 보장될 때, 그 시점에서의 최적을 구하는 과정을 반복하는 방법론이 있는 걸로 기억한다. 정확한 명칭은 기억이 안나지만서도;; -_-;;
그렇다. Dijkstra’s Algorithm역시, 이런 방법에 기초하고 있다. 헌데 가만히 생각해 보면,
이것은 부분최적이(이런말 있나 -__-;;;) 전체 최적이다라고 할수 있을 때 가치가 있다.
먼가 Fixed된 것이다. 즉, Network으로 애기하면, 망이 변화지 않는다. 즉, traffice같은 망의 정보, 지연시간 같은 망의 정보가 변화하지 않고 Fixed라고 했을 때 유용한 것이다.
다시 말해, 정적 라우팅인 것이다.
앞서 Bellman-Ford’s Algorithm이 Dynamic Routing인 것에 비해 말이다.

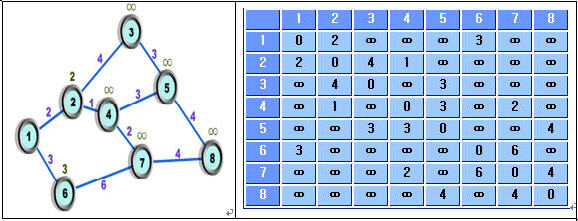
Picture 4. Example for understanding about Dijkstra’s Algorithm
위와 같은 Subnet이 있다고 할 때, 어떤 한 Source Node에서 Destination Node까지의 최단 경로와 거리를 Dijkstra사마의 제안에 따라 해결해 보자 -_-;;
지금부터의 순차적인 그림 설명을 따라가다 보면 다음 행렬의 의미를 이해할 수 있다.
int data[8][8]= {
{0,2,m,m,m,3,m,m},
{2,0,4,1,m,m,m,m},
{m,4,0,m,3,m,m,m},
{m,1,m,0,3,m,2,m},
{m,m,3,3,0,m,m,4},
{3,m,m,m,m,0,6,m},
{m,m,m,2,m,6,0,4},
{m,m,m,m,4,m,4,0} };
먼저 설명을 하면, m은 너무 큰 Integer즉, 숫자인데 이는 “너무 멀다 그래서 갈수 없다 거리를 알수 없다”의 의미로 이해하면 된다.
Data[i][j]의 기본 사용용도는, Node i에서 Node j까지 가는데 걸리는 거리다.
허나!!!!! 이는 최소 최단 거리라는 말은 결코 아니다.
저런 matrix를 인접행렬이라고 한다.
실제 이 인접행렬을 망을 딱보고 어떻게 만들수 있을까 생각해 낼 수가 있다면,
기본을 잡고 들어가는 거라 생각한다.
위의 망형태와 다소 다른 다음 그림을 보고 똑같이 matrix를 만들어 보자.
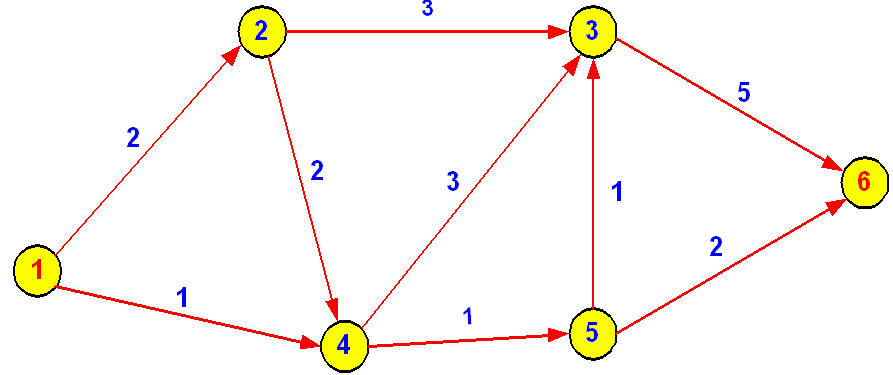
Picture 5. Another Example for understanding about Dijkstra’s Algorithm
int data[8][8]= {
{0,2,m,1,m,m},
0 -> 처음 시작 Node인 1에서 1까지의 거리는 당연히 0이다.
인접 Node인 2로 가는 경우 거리는 2이다.
Node 3으로 가는 것은(이때의 Source Node는 1인 경우다 주의하라!!)
5일까? 아니다. m이다 즉, 큰 수이다. 즉, 알수없다 내지는 너무 멀다로 취급한다.
Node 4는? 1이 된다.
Node 5는? 역시 m Node 6은? 역시 m이다.
감이 올 것이다. 즉, 인접노드만이 거리를 알수 있는 것이고(이때 최소 최단거리의 의미는 아직은 결코 아니다.!!) 나머지는 알수없다 너무멀다의 의미로 취급하기 위해 충분히 큰 수로 define된 m을 사용한다. 마찬 가지로, 나머지에 대해서도 해보자.
{2,0,3,2,m,m},
자 이번엔 Source Node를 2라고 한다. 다음으로 1,3,4,5,6 Node에 대한 거리를 계산하려 하는데, 앞서 애기되로 Dijkstra’s Algorithm에서는 인접 Node를 제외하고는 모두 너무 멀다일 뿐이다. 따라서 위와 같이 된다..
이를 3,4,5,6에 대해서 모두 적용시켜 보자.
{m,3,0,3,1,5}, Node 3번에서
{1,2,3,0,1,m}, Node 4번에서
{m,m,1,1,0,2}, Node 5번에서
{m,m,5,m,2,0}, Node 6번에서
계속 반복하지만, 그 시점에서 최적인 것 이말은, 인접노드에 대한 거리만을 생각하여 최소의 거리를 구하고 그때의 Node를 알고 이 모든 부분부분 계산을 더해 결과적인 것이 최적이다라고 할 수가 있다고 할때에, 각각의 최소거리의 총합이 목적 Node까지의 최소거리가 되며, 그때 그때 선택한 Node로 인해 치소거리 즉, 최단거리 최적 경로가 결정되는 것이다.
위 인접행렬은 아직 각각의 Node에서의 인접 Node까지의 거리정보만을 보여준다.
하지만, 그 인접노드의 거리 정보를 모두 보여주고 있다.
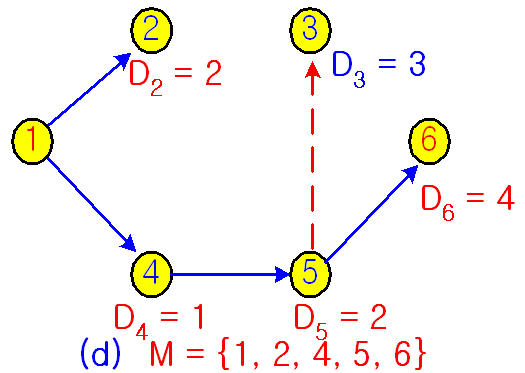
Picture 5. The process of Dijkstra’s Algorithm
누누히 애기하지만, 그 시점 그 Node에서의 최소거리를 선택해나간다 쭉 ~~~~~~
M은 바로 그때 그때 최적 경로선택을 할때마다의 그 Node인 것이다.
처음에는 인접 Node인 4와 2가 M에 포함되지만, 2에서 6으로 가기위해서 인접 Node인 4와 3방향 거리값이 4에서 인접 Node인 5로 가는 거리보다 크므로, 4다음에 M에 속하는 Node는 5가 된다. 역시 이제 5에서 생각한다 5의 인접노드는 6으로 바로 가는 것과 3을
거치는 것이 있는데, 6으로 바로 가는 것이 더 작은 거리이므로 6을 선택한다.
최종적으로 6이 선택되었으므로, 1->6으로 경로에 필요한 M이 완성되는 것이다.
이제 이 Table을 이해할 수가 있을 것이다.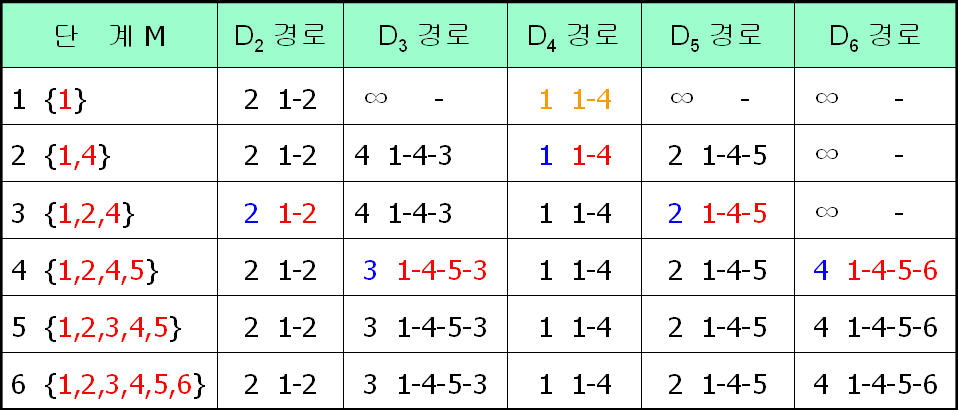
Table 3. Table to Route from Node 1 to Node 6 in using Dijkstra’s Algorithm
Dijkstra’s Algorithm은 솔직히 매우 우수하다고는 볼수가 없다.
현대의 Network는 동적이기 때문이다. 수시로 각 노드간의 Delay값과 Routing정보는 바뀌는 것이다. 하지만, 어느 책에선가, 이 Algorithm이 중요한 base가 된다는 것을 읽은 기억이 있다. 특히 AD-HOC에서 말이지.. 음
사람들 중에는 눈앞의 이익만을 생각한 나머지 다가올 수 있었던 더 큰이익을 눈치채지 못하는 경우가 있다.
이 알고리즘또한 그러하다. 어느 순간의 최적이 있다고 볼 때, 그 최적의 합이 결국 최종적인 최적을 의미할수 있다고 전제될 수가 있을 때 유용한 것이다.
Picture 6. example of Dijkstra’s Algorithm
Source node를 1이라고 하고, Destination Node를 8이라고 할 때, 인접배열을 위한 table이 위처럼 작성될 수가 있다.
처음 1의 입장에서 2와 6은 인접해 있기에 그 거리를 기록할 수가 있다. 즉 알수 있다고 보는 것이다. 이에 반해서, 나머지 node는 보이지 않는다. 아득한 거리로 보자는 것이다.
역시 만약 2번 path를 타기로 결정했다면, 2에서 볼 때, 1,3,4를 제외하고는 아득한 거리가 되버린다. 바로 이런식의 패턴이 Dijkstra’s Algorithm의 concept이다.
Dijkstra’s Alogorithm에 대한 글을 읽다가 보면, 최단거리를 기록해 가다가 좀 더 작은 값이 나오게 되면 이를 갱신한다라는 말이 많다.
이 의미는 다음과 같다.
4에서 거리가 결정되는 것은 5와 7이다. 이때, 다른 path인 6을 타는 경로에서 7이 또 결정될수가 있다. 즉, 4를 타는 path에서의 최단거리의 총합 이때의 기준은 그 시점에서의 최종 node이다. 즉 여기선 4이다. 헌데, 최종node가 7인 path를 타려하는 것이다.
최종이 7이되면, 최단거리는 5가 된다. 헌데, 6번을 탔을 경우 그 값이 9가되어 최단거리는 갱신되지 못할 것이다. 즉 node 7까지 왔을 때 물론, 이때는 최단거리 경로를 탔을 것이다.
그 값이 5가 된다. 그리고 이놈은 fixed된다. 이것이 영구 값이 되는 것이다.
순간 순간 시점에서의 즉, 최종node를 바꿔가면서 실제의 최종node를 찾아가되 각각의 step에서, 최단거리 값을 기록해 가는 것이다.그러면서, 최단거리값이 제일 작은 것이 계속적으로 setting되다가, 최종적으로는 영구값이 될 것이다.
여기서 우리는 이것이 Dynamic Routing이 되지 못함을 또한 알수가 있다.
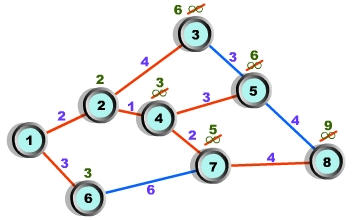
Picture 7. example of Dijkstra’s subnet?^^
따라서 이제, 1->2->4->7->8 path가 이 subnet에서 from 1 to 8의 최단거리 경로가 됨을 알 수가 있다.
Dijkstra’s Alogorithm은 이처럼 순간수간 중간최종node에서의 최단거리 값의 결정에 대한 조사가 이루어지는 것이다.
4번에서 7로 가는 것말고도 5로 갈수도 있었을 것이다 하지만, 이럴경우
2+1+3+4 > 2+1+2+4가 되어 결국 node 8의 최단거리 값은 수정되지 않고 fixed된다.
이런 subnet은 traffic이나, 최소 전송 Delay time등을 고려하지 못하는 것이다.
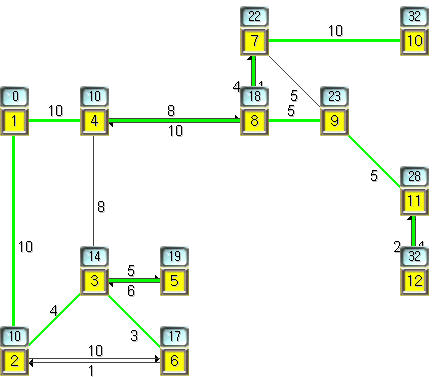
Picture 8. point and time to select
Node 1에서 Node 12로 가는 경로에서의 최소거리 Routing을 하고싶다고 하자.
먼저 위에서 선택의 시점이 몇번 온다고 생각할 수가 있을까?
6번이다.
Node 1에서 선택해야 한다.
Node 2에서 선택해야 한다.
Node 3에서 선택해야 한다.
Node 4에서 선택해야 한다.
Node 8에서 선택해야 한다.
Node 7에서 선택해야 한다.
혹여, Node 2,3에서나, Node 7에서의 선택을 왜 해야하냐고 반문할 수가 있겠으나,
그건 아마도 최적의 경로상에서의 선택이 아니기 때문일것이다.
하지만, 그건은 답을 알고 풀이과정을 그것에 맞추는 것이다.
Dijkstra’s Alogorithm으로 문제를 푼다고 할 때, 설사 그림상 빙 돌아가는 듯 하여도
반드시 거리가 조사되어야 한다. 빙 돌아가는 것이 오히려 최단거리 최적루트가 될수도 있기때문이다. 심지어 다음의 경우도 있다.
Node 4에서의 최단거리의 합이 결정났다고 했을 때, Node 4에서는 3과 8의 루트를 가질수가 있겠으나, 이때 거리가 +8로써 같기에, 이 경우는 단순히 선택의 차원이 넘어서서
최단거리 계산반영에 까지 이어지게 된다. 즉 일단 내려갔다가 다시 4로 돌아와서의 최단거리 합이 계산되어서 이것이 더 크다고 판명이 날때까지인 것이다.
중요한 것은 반드시 인접 노드가 2개 이상일 때, 그 거리의 값이 동일했다면, 단순히 조사를 하여 선택할수 있는 것이 아니라, 설사 결과적으로는 최적루트상의 root가 아니었다고 하여도, 그 노드로 가는 path를 검사하여 다시 돌아왔을 시점에서의 최단거리 값을 구하여야 한다. 여기서 그 값이 설정된 값보다 크다고 판명날 때 이쪽 path가 아님을 인지하는 것이다. 물론 이런 세세한 부분은 프로그램의 방향에 따라 다소 다를수 있겠다 싶다.
머리속의 내용을 설명하기가 쉽진않다.
거리를 조사한다와 조사한 거리를 더하여 크기를 비교한다의 개념을 난 구분해서 사용했음을 알려드린다.
그렇다면, 결국 최소거리는 몇일까?
32이다. 금방 알 수 있을 것이다.
'Module > Algorithm' 카테고리의 다른 글
| [Algorithm] A star(A*) (0) | 2010.10.14 |
|---|---|
| Hermite spline (0) | 2008.11.26 |
| 다익스트라(Dijkstra) 알고리즘 (0) | 2008.10.09 |